Quantifications of Intensity-Modulated Radiation Therapy Plan Complexities in Magnetic Resonance Image Guided Radiotherapy Systems

Minsoo Chun; Ohyun Kwon; Jong Min Park; Jung-in Kim

doi:10.14407/jrpr.2020.00290

J. Radiat. Prot. Res > Volume 46(2); 2021 > Article

Chun, Kwon, Park, and Kim: Quantifications of Intensity-Modulated Radiation Therapy Plan Complexities in Magnetic Resonance Image Guided Radiotherapy Systems

Original Research

Journal of Radiation Protection and Research 2021; 46(2): 48-57.

Published online: June 30, 2021

DOI: https://doi.org/10.14407/jrpr.2020.00290

Quantifications of Intensity-Modulated Radiation Therapy Plan Complexities in Magnetic Resonance Image Guided Radiotherapy Systems

Minsoo Chun^1,^2,³, Ohyun Kwon⁴, Jong Min Park^1,^2,^3,⁵, Jung-in Kim^1,^2,³

¹Department of Radiation Oncology, Seoul National University Hospital, Seoul, Korea

²Biomedical Research Institute, Seoul National University Hospital, Seoul, Korea

³Institute of Radiation Medicine, Seoul National University Medical Research Center, Seoul, Korea

⁴Department of Medical Physics, University of Wisconsin, Madison, WI, USA

⁵Department of Radiation Oncology, Seoul National University College of Medicine, Seoul, Korea

Corresponding author: Jung-in Kim, Department of Radiation Oncology, Seoul National University Hospital, 101 Daehak-ro, Jongno-gu, Seoul 03080, Korea, E-mail: madangin@gmail.com, https://orcid.org/0000-0002-0305-5969

Received December 21, 2020 Revised January 19, 2021 Accepted February 16, 2021

This is an open-access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by-nc/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Background

In this study, the complexities of step-and-shoot intensity-modulated radiation therapy (IMRT) plans in magnetic resonance-guided radiation therapy systems were evaluated.

Materials and Methods

Overall, 194 verification plans from the abdomen, prostate, and breast sites were collected using a ⁶⁰Co-based ViewRay radiotherapy system (ViewRay Inc., Cleveland, OH, USA). Various plan complexity metrics (PCMs) were calculated for each verification plan, including the modulation complexity score (MCS), plan-averaged beam area (PA), plan-averaged beam irregularity, plan-averaged edge (PE), plan-averaged beam modulation, number of segments, average area among all segments (AA/Seg), and total beam-on time (TBT). The plan deliverability was quantified in terms of gamma passing rates (GPRs) with a 1 mm/2% criterion, and the Pearson correlation coefficients between GPRs and various PCMs were analyzed.

Results and Discussion

For the abdomen, prostate, and breast groups, the average GPRs with the 1 mm/2% criterion were 77.8±6.0%, 79.8±4.9%, and 84.7±7.3%; PCMs were 0.263, 0.271, and 0.386; PAs were 15.001, 18.779, and 35.683; PEs were 1.575, 1.444, and 1.028; AA/Segs were 15.37, 19.89, and 36.64; and TBTs were 18.86, 19.33, and 5.91 minutes, respectively. The various PCMs, i.e., MCS, PA, PE, AA/Seg, and TBT, showed statistically significant Pearson correlation coefficients of 0.416, 0.627, −0.541, 0.635, and −0.397, respectively, with GPRs.

Conclusion

The area-related metrics exhibited strong correlations with GPRs. Moreover, the AA/Seg metric can be used to estimate the IMRT plan accuracy without beam delivery in the ⁶⁰Co-based ViewRay radiotherapy system.

Keywords: MRI-Guided Radiotherapy System, Step-and-Shoot Intensity-Modulated Radiation Therapy, Gamma Analysis, Plan Complexity Metric

Introduction

Although intensity-modulated radiation therapy (IMRT) delivers prescription doses to target volumes while sparing the normal tissues [1–3], it is often associated with high degrees of modulations including severe multi-leaf collimator (MLC) movements, numerous monitor units (MUs), and the frequent use of small and irregular beam apertures [4–6]. This complicated treatment techniques may cause both delivery errors and dose calculations [7–9]. Therefore, the accuracy of the plan delivery should be verified in advance of the treatment, and a gamma evaluation has been widely adopted as a pre-treatment quality assurance (QA) [10, 11]. While gamma analysis is practical by comparing the calculated and measured dose distributions, there exists several limitations such as clinical irrelevances and consumptions of human and clinical resources [12–14]. To substitute or support the gamma analysis platform, several studies have attempted to characterize degrees of plan modulation for IMRT and volumetric modulated arc therapy (VMAT) plans [4, 6, 7, 15–17].

IMRT and VMAT are known to be capable of allowing dose escalation and reduced toxicity to the organs at risk when compared with three-dimensional (3D) conformal radiation therapy [18, 19]. Although step-and-shoot (SS) IMRT is less complex [19], many studies have attempted to quantify the degree of modulation and complexity for the SS IMRT plans. McNiven et al. [4] suggested the modulation complexity score (MCS) to quantify the complexity and deliverability of SS IMRT plans, and reported improved sensitivity using the MCS compared with the number of MUs. Du et al. [15] devised the plan-averaged area (PA), the plan-averaged irregularity (PI), the plan-averaged modulation (PM), and plan-normalized monitor unit metrics to evaluate the complexity of the SS IMRT plans quantitatively. They demonstrated a negative correlation between the minimum segment area and PM, indicating that the small beam apertures in spine stereotactic plans could induce large discrepancies between the planned and measured doses. The complexity of the created static MLC openings (defined as regions with 5% dose difference between the measurement and calculation), devised by Gotstedt et al. [20], was correlated to the aperture-based complexity metrics and dependent on the penumbra region relative to the area of the opening.

Recently, the introduction of magnetic resonance-guided radiation therapy (MRgRT) has enabled real-time respiratory gating without an external surrogate [21–24]. The ViewRay system (ViewRay Inc., Cleveland, OH, USA) is the world’s first commercial MRgRT system that integrates an MR imaging system, a radiation therapy (RT) delivery system, and an integrated treatment planning system [22–25]. The RT system consists of three ⁶⁰Co heads (120° apart), each of which is equipped with 60 double-focused MLCs without collimator jaws, with the beams delivered using the SS technique [22–26]. While this unique beam delivery method emphasizes the quantification of the plan complexity, this has rarely been studied for the ⁶⁰Co-based ViewRay system to date. Owing to the distinctive process of beam delivery and unique collimator geometry, i.e., 60 double-focused MLCs without a primary collimator [22–26], those dedicated to the ViewRay system should be individually evaluated. Recently, Liu et al. [26] attempted to quantify the treatment plan complexity for this system, demonstrating a linear relationship between the total treatment time and PM.

Due to current pre-treatment QA mostly relies on the measurement-based gamma analysis, estimation of gamma passing rate (GPR) with complexity metrics could provide foresights in terms of accurate delivery. When plans with low GPR estimation, they can be modified without actual QA beam delivery. The increased use of adaptive RT, especially in MRgRT systems, also necessities the prediction of the GPR in advance of treatment [27, 28]. The online adaptive plan has different plan parameters compared with the initial plan such as gantry angles, segment shapes, and beam-on times, whose deliverability should be re-verified by comparing the recalculated dose distribution and delivery for the re-optimized plan. However, the fraction-specific QA for each adaptive plan is impractical due to potential anatomical changes when the patient is transferred from the table [29–32].

In this study, we evaluated various plan complexity metrics (PCMs) subject to the SS IMRT in the MRgRT system with a relatively large number of dataset in multiple disease groups. The impacts of PCMs on delivery accuracies were demonstrated with correlation analysis across PCMs, GPRs, and parameter differences between planned and actual parameters.

Materials and Methods

1. Data Selection and Treatment Planning

Following approval by the Institutional Review Board of Seoul National University Hospital (No. 1906-061-1039), 194 verification plans from 113 patients were retrospectively collected in this study. Treatment sites included abdomen, prostate, and breast cancer patients. Abdomen and prostate cancer patients were treated with stereotactic ablative body radiotherapy (SABR) schemes, while breast cancer patients were consisted of accelerated partial breast irradiation (APBI) plans with hypofractionated IMRT. Patients with pancreatic and liver cancers are categorized into abdomen groups.

All patients were scanned with the Brilliance CT Big Bore (Phillips, Amsterdam, The Netherlands) and ViewRay 0.35 T magnetic resonance imaging system on the same day. The computed tomography (CT) images were rigidly deformed to MR images for dose calculations with an electron density map. The treatment plans were established using the MRIdian treatment planning system (ViewRay Inc.) with the SS IMRT techniques. The value of IMRT efficiency was set to 0.5, and prescriptions and optimization objectives were described as follows. For abdomen groups, the initial prescription dose was 50 Gy in five fractions. If any of doses received by 1 cc volume (D_1cc) of a duodenum, a bowel, and a stomach exceeded 33 Gy, the prescription dose was reduced until their tolerance levels were met and optimization was repeated [33]. Also, dose-volumetric constraints of D_15cc less than 32 Gy for a heart and D_700cc less than 21 Gy for a normal liver were applied [34, 35]. For prostate cancer patients, the prescription dose was 36.25 Gy in five fractions, and volume receiving more than 100% of the prescription dose (V_100%), V_90%, V_80%, and V_50% less than 5%, 10%, 20%, and 50%, respectively, were used for bowel constraints [33]. For breast cancer patients, they were prescribed by 38.5 Gy in 10 fractions, and constraints of V_20Gy less than 20% for an ipsilateral lung, and mean dose less than 10 Gy for a heart were applied [35].

The verification plans were then generated by replacing patients’ images with the MR-compatible ArcCHECK (Sun Nuclear Corp., Melbourne, FL, USA) phantom images. The reference dose distributions were calculated by using a Monte Carlo simulation-based dose calculation algorithm with a 3 mm grid resolution supported by the MRIdian treatment planning system. Calculations with magnetic field option were applied.

2. Measurements and Gamma Analysis

Each dose distribution was measured with the MR-compatible ArcCHECK consisting of the SunPoint diode detector (Sun Nuclear Corp.). The spacing and active volume of the detector are 10 mm and 0.019 mm³, respectively. Prior to the measurements, array calibration and absolute dose calibration of the ArcCHECK were performed according to the manufacturer’s calibration procedure. Two-dimensional gamma analysis was performed using the SNC patient software (version 6.6; Sun Nuclear Corp.) with a 10% threshold. The dose distribution was automatically interpolated with 1 mm dose grid in the software. The global gamma analysis was performed with gamma criterion of 1 mm/2%.

3. Plan Complexity Metrics

As the radiation isotope (⁶⁰Co) is used as a source of the ViewRay system, the beam delivery is governed by the beam-on time. In this study, to account for this property in the PCMs, the MU weighting factor in the initial definition was replaced by the time weighting factor to emphasize the segment and the field with a longer beam-on time. Each plan consists of multiple gantry angles called as “field,” which possess their own beam aperture shapes (segment). In Table 1, the modified definitions of the PCMs are summarized with respect to the segment phases, field phases, and plan phases.

MCS suggested by McNiven et al. [4], and PA, PI, plan-averaged edge (PE), and PM suggested by Du et al. [15], and Younge et al. [36] were utilized. Same as characteristics of the initial definitions, plans with high complexity possessed low MCS and PA values, and high PI, PE, and PM. In additions, an average aperture area per each segment (AA/Seg), and total beam-on time (TBT) along with total beam-on time per daily dose (Time/DD) were analyzed. To investigate the impact of segments with small area, and short beam-on time, the percent proportion of segment with beam-on times less than 3, 5, and 10 seconds (%Time/Seg<3, %Time/Seg<5, and %Time/Seg<10), and average areas among all segments less than 2.5, 5.0, 7.5, and 10.0 cm² (%SA/Seg<2.5, %SA/Seg<5.0, %SA/Seg<7.5, and %SA/Seg<10.0) were used for analysis [37].

4. Statistical Analysis

To find the significant differences on PCMs, F-test was firstly performed to determine whether two values possess an equality of variances, and then t-test was followed to find the statistical significances. The Pearson correlation coefficient between GPRs and various PCMs were calculated. Only coefficients with statistical significances (p<0.001) are presented.

Results and Discussion

The GPRs with a 1 mm/2% criterion were 77.8±6.0%, 79.8± 4.9%, and 84.7±7.3%, for abdomen, prostate, and breast groups, respectively. Breast IMRT plans exhibited significantly higher GPRs than those of all the other SABR plans, on average. It seems appropriate for SNC software interpolates the calculated dose distribution with 1 mm grid as gamma analysis between the dose distribution calculated with 2.5 mm grid (1.25 mm interpolation) and 1.25 mm grid showed 97.9% GPRs by using 1% and 0.1 mm criterion, and 0% threshold [38].

The representative aperture shapes along with the aperture area (AA), the aperture irregularity (AI), the aperture edge (AE), and the time weighting factor for each segment in the abdomen SABR plans are presented in Fig. 1. The abdomen SABR plan exhibited higher complexity than the APBI IMRT plans with smaller and much irregular beam apertures, resulting in a lower beam area metric (BA) and higher beam irregularity (BI), beam edge (BE), and beam modulation (BM) in the field phase.

Statistics for PCMs according to the treatment sites, along with statistical significances in PCMs between breast IMRT and SABR groups, and those between abdomen SABR and prostate SABR groups were also provided. Breast IMRT plans showed the statistically higher MCS, PA, and AA/Seg, and lower PI, PE, PM, TBT, and Time/DD compared to SABR plans (Table 2).

The Pearson correlation coefficients between various PCMs and GPRs with a 1 mm/2% criterion are presented in Table 3, and scatter plots were provided in Fig. 2. The majority of PCMs showed significant correlations with GPRs except for PI, PM, and #Seg. The majority of area-related metrics such as PA, PE, AA/Seg, %SA/Seg<2.5, %SA/Seg<5.0, %SA/Seg<7.5, and %SA/Seg<10.0 showed significant correlations with GPRs (p<0.001). Furthermore, segments containing short beam-on time also showed significant correlations with GPRs (p<0.001). A strongest correlation with the GPR was occurred with AA/Seg metric showing Pearson correlation coefficient of 0.635.

Study results revealed area-related metrics tended to possess strong correlations with GPRs. In small fields, the accuracies of calculations and measurements became could become poor due to the lack of lateral charged particle equilibrium and overlapping penumbras [39–41]. As several researches reported the presence of the MR could impact the dosimetric performances [42–45], the inaccuracies in small fields might also be occurred same as the absence of the MR fields [46]. When using highly modulated fields with large number of small segments, inaccurate output factors may cause uncertainties in dose calculation [47]. Our study results showed concordant tendencies with previous studies showing plans with small PA or AA/Seg possessed low GPRs. Specifically, those impacts are more powerful than those with time parameters.

Despite the lack of contradictory correlation tendencies compared to another literature, the correlation strength between the PCMs and GPRs was relatively low [5]. This might be because the number of fields was greater than that reported in a previous study [5], which in turn resulted in the complexity for each field being potentially smeared out by utilizing higher number of fields. Future studies will focus on a more precise and direct evaluation of the plans only consisting of complex beam apertures. Even so, the study outcomes present the large proportion of segments with small apertures and short beam-on times might reduce the deliverability of the plans.

Most previous studies on patient-specific QA for online adaptive RT plans did not perform a conventional measurement-based QA. In the study by Acharya et al. [29], their in-house QA tools provided comparisons of important plan parameters between initial and re-optimized plans along with independent Monte Carlo-based dose calculations and 3D gamma analysis [48]. Lamb et al. [49] discussed the challenges of measurement-based QA for online adaptive plans due to potential alternations in the anatomy when the patient is transferred from the table. They retrospectively delivered 20 plans of adaptive fractions to a QA phantom, all of which passed the tolerance level (i.e., >95% GPR with a 3 mm/3% criterion). An automated process to check the consistency of contour volumes, segment beam-on time, and dose-volumetric parameters is also a meaningful approach to mitigate unexpected errors [49]. Several alternative approaches in fraction-specific measurement-based QA are routinely used clinically or are under investigation such as secondary dose calculations, automated parameter comparisons between the initial and re-optimized plans, and MR-compatible electronic portal imaging detector-based QA workflows [29, 30, 48, 50].

Although ⁶⁰Co ViewRay system has been replaced to magnetic resonance linear accelerator (MR-Linac) system recently, there are still several institutions using this system. Furthermore, the study outcomes highlights that the large amount of small segment aperture could aggravate the plan delivery accuracy, which can also be applied in all SS IMRT with MR-Linac system.

Conclusion

The area-related metrics, such as PA, AA/Seg, and average areas less than specific area, exhibited the strong correlations with GPRs. As all metrics can be obtained at the planning stage, plans with small AA/Seg might be modified without actual plan delivery in the ⁶⁰Co-based MRgRT system.

Notes

Conflict of Interest

No potential conflict of interest relevant to this article was reported.

Author Contribution

Conceptualization: Chun M. Data curation: Kwon O. Formal analysis: Kwon O. Funding acquisition: Chun M. Methodology: Chun M. Visualization: Kwon O. Writing - original draft: Chun M. Writing - review & editing: Park JM, Kim J. Investigation: Kim J. Resources: Kwon O. Software: Chun M. Supervision: Park JM, Kim J. Validation: Chun M, Kwon O.

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (No. NRF-2019R1F1A1041944).

References

1. Kim YS, Lee J, Park JI, Sung W, Lee SM, Kim GE. Volumetric modulated arc therapy for carotid sparing in the management of early glottic cancer. Radiat Oncol J. 2016;34:18-25.

2. Sung W, Park JM, Choi CH, Ha SW, Ye SJ. The effect of photon energy on intensity-modulated radiation therapy (IMRT) plans for prostate cancer. Radiat Oncol J. 2012;30:27-35.

3. Kim SJ, Youn SM, Kim SK. A dosimetric comparision of IMRT and VMAT in synchronous bilateral breast cancer. Prog Med Phys. 2013;24:284-289.

4. McNiven AL, Sharpe MB, Purdie TG. A new metric for assessing IMRT modulation complexity and plan deliverability. Med Phys. 2010;37:505-515.

5. Park SY, Kim JI, Chun M, Ahn H, Park JM. Assessment of the modulation degrees of intensity-modulated radiation therapy plans. Radiat Oncol. 2018;13:244.

6. Chun M, An HJ, Kwon O, Oh DH, Park JM, Kim JI. Impact of plan parameters and modulation indices on patient-specific QA results for standard and stereotactic VMAT. Phys Med. 2019;62:83-94.

7. Park SY, Kim IH, Ye SJ, Carlson J, Park JM. Texture analysis on the fluence map to evaluate the degree of modulation for volumetric modulated arc therapy. Med Phys. 2014;41:111718.

8. Cilla S, Meluccio D, Fidanzio A, Azario L, Ianiro A, Macchia G, et al. Initial clinical experience with Epid-based in-vivo dosimetry for VMAT treatments of head-and-neck tumors. Phys Med. 2016;32:52-58.

9. Arumugam S, Xing A, Young T, Holloway L. Sensitivity of a helical diode array dosimeter to volumetric modulated arc therapy delivery errors. Phys Med. 2015;31:1043-1054.

10. Ezzell GA, Burmeister JW, Dogan N, LoSasso TJ, Mechalakos JG, Mihailidis D, et al. IMRT commissioning: multiple institution planning and dosimetry comparisons, a report from AAPM Task Group 119. Med Phys. 2009;36:5359-5373.

11. Miften M, Olch A, Mihailidis D, Moran J, Pawlicki T, Molineu A, et al. Tolerance limits and methodologies for IMRT measurement-based verification QA: recommendations of AAPM Task Group No. 218. Med Phys. 2018;45:e53-e83.

12. Stasi M, Bresciani S, Miranti A, Maggio A, Sapino V, Gabriele P. Pretreatment patient-specific IMRT quality assurance: a correlation study between gamma index and patient clinical dose volume histogram. Med Phys. 2012;39:7626-7634.

13. Nelms BE, Zhen H, Tome WA. Per-beam, planar IMRT QA passing rates do not predict clinically relevant patient dose errors. Med Phys. 2011;38:1037-1044.

14. Palaniswaamy G, Scott Brame R, Yaddanapudi S, Rangaraj D, Mutic S. A statistical approach to IMRT patient-specific QA. Med Phys. 2012;39:7560-7570.

15. Du W, Cho SH, Zhang X, Hoffman KE, Kudchadker RJ. Quantification of beam complexity in intensity-modulated radiation therapy treatment plans. Med Phys. 2014;41:021716.

16. Park JM, Kim JI, Park SY. Modulation indices and plan delivery accuracy of volumetric modulated arc therapy. J Appl Clin Med Phys. 2019;20:12-22.

17. Park JM, Kim JI, Park SY, Oh DH, Kim ST. Reliability of the gamma index analysis as a verification method of volumetric modulated arc therapy plans. Radiat Oncol. 2018;13:175.

18. De La Fuente Herman T, Schnell E, Young J, Hildebrand K, Algan O, Syzek E, et al. Dosimetric comparison between IMRT delivery modes: step-and-shoot, sliding window, and volumetric modulated arc therapy: for whole pelvis radiation therapy of intermediate-to-high risk prostate adenocarcinoma. J Med Phys. 2013;38:165-172.

19. Elith C, Dempsey SE, Findlay N, Warren-Forward HM. An Introduction to the intensity-modulated radiation therapy (IMRT) techniques, tomotherapy, and VMAT. J Med Imaging Radiat Sci. 2011;42:37-43.

20. Gotstedt J, Karlsson Hauer A, Back A. Development and evaluation of aperture-based complexity metrics using film and EPID measurements of static MLC openings. Med Phys. 2015;42:3911-3921.

21. Mittauer K, Paliwal B, Hill P, Bayouth JE, Geurts MW, Baschnagel AM, et al. A new era of image guidance with magnetic resonance-guided radiation therapy for abdominal and thoracic malignancies. Cureus. 2018;10:e2422.

22. Mutic S, Dempsey JF. The ViewRay system: magnetic resonance-guided and controlled radiotherapy. Semin Radiat Oncol. 2014;24:196-199.

23. Wooten HO, Rodriguez V, Green O, Kashani R, Santanam L, Tanderup K, et al. Benchmark IMRT evaluation of a Co-60 MRI-guided radiation therapy system. Radiother Oncol. 2015;114:402-405.

24. Pollard JM, Wen Z, Sadagopan R, Wang J, Ibbott GS. The future of image-guided radiotherapy will be MR guided. Br J Radiol. 2017;90:20160667.

25. Wooten HO, Green O, Yang M, DeWees T, Kashani R, Olsen J, et al. Quality of intensity modulated radiation therapy treatment plans using a ⁶⁰Co magnetic resonance image guidance radiation therapy system. Int J Radiat Oncol Biol Phys. 2015;92:771-778.

26. Liu S, Wu Y, Wooten HO, Green O, Archer B, Li H, et al. Methods to model and predict the ViewRay treatment deliveries to aid patient scheduling and treatment planning. J Appl Clin Med Phys. 2016;17:50-62.

27. Bohoudi O, Bruynzeel AM, Senan S, Cuijpers JP, Slotman BJ, Lagerwaard FJ, et al. Fast and robust online adaptive planning in stereotactic MR-guided adaptive radiation therapy (SMART) for pancreatic cancer. Radiother Oncol. 2017;125:439-444.

28. Hunt A, Hansen VN, Oelfke U, Nill S, Hafeez S. Adaptive radiotherapy enabled by MRI guidance. Clin Oncol (R Coll Radiol). 2018;30:711-719.

29. Acharya S, Fischer-Valuck BW, Kashani R, Parikh P, Yang D, Zhao T, et al. Online magnetic resonance image guided adaptive radiation therapy: first clinical applications. Int J Radiat Oncol Biol Phys. 2016;94:394-403.

30. Boldrini L, Cusumano D, Cellini F, Azario L, Mattiucci GC, Valentini V. Online adaptive magnetic resonance guided radiotherapy for pancreatic cancer: state of the art, pearls and pitfalls. Radiat Oncol. 2019;14:71.

31. Tetar SU, Bruynzeel AM, Lagerwaard FJ, Slotman BJ, Bohoudi O, Palacios MA. Clinical implementation of magnetic resonance imaging guided adaptive radiotherapy for localized prostate cancer. Phys Imaging Radiat Oncol. 2019;9:69-76.

32. Li HH, Rodriguez VL, Green OL, Hu Y, Kashani R, Wooten HO, et al. Patient-specific quality assurance for the delivery of ⁶⁰Co intensity modulated radiation therapy subject to a 0.35-T lateral magnetic field. Int J Radiat Oncol Biol Phys. 2015;91:65-72.

33. Hanna GG, Murray L, Patel R, Jain S, Aitken KL, Franks KN, et al. UK Consensus on normal tissue dose constraints for stereotactic radiotherapy. Clin Oncol (R Coll Radiol). 2018;30:5-14.

34. Benedict SH, Yenice KM, Followill D, Galvin JM, Hinson W, Kavanagh B, et al. Stereotactic body radiation therapy: the report of AAPM Task Group 101. Med Phys. 2010;37:4078-4101.

35. Marks LB, Yorke ED, Jackson A, Ten Haken RK, Constine LS, Eisbruch A, et al. Use of normal tissue complication probability models in the clinic. Int J Radiat Oncol Biol Phys. 2010;76(3 Suppl):S10-S19.

36. Younge KC, Matuszak MM, Moran JM, McShan DL, Fraass BA, Roberts DA. Penalization of aperture complexity in inversely planned volumetric modulated arc therapy. Med Phys. 2012;39:7160-7170.

37. Shen L, Chen S, Zhu X, Han C, Zheng X, Deng Z, et al. Multidimensional correlation among plan complexity, quality and deliverability parameters for volumetric-modulated arc therapy using canonical correlation analysis. J Radiat Res. 2018;59:207-215.

38. Hussein M, Clark CH, Nisbet A. Challenges in calculation of the gamma index in radiotherapy: towards good practice. Phys Med. 2017;36:1-11.

39. Han T, Mikell JK, Salehpour M, Mourtada F. Dosimetric comparison of Acuros XB deterministic radiation transport method with Monte Carlo and model-based convolution methods in heterogeneous media. Med Phys. 2011;38:2651-2664.

40. Sanchez-Doblado F, Hartmann GH, Pena J, Rosello JV, Russiello G, Gonzalez-Castano DM. A new method for output factor determination in MLC shaped narrow beams. Phys Med. 2007;23:58-66.

41. Sendani NG, Karimian A, Mahdavi SR, Jabbari I, Alaei P. Effect of beam configuration with inaccurate or incomplete small field output factors on the accuracy of treatment planning dose calculation. Med Phys. 2019;46:5273-5283.

42. Cervantes Y, Billas I, Shipley D, Duane S, Bouchard H. Small-cavity chamber dose response in megavoltage photon beams coupled to magnetic fields. Phys Med Biol. 2020;65:245008.

43. Lehmann J, Beveridge T, Oliver C, Bailey TE, Lye JE, Livingstone J, et al. Impact of magnetic fields on dose measurement with small ion chambers illustrated in high-resolution response maps. Med Phys. 2019;46:3298-3305.

44. O’Brien DJ, Roberts DA, Ibbott GS, Sawakuchi GO. Reference dosimetry in magnetic fields: formalism and ionization chamber correction factors. Med Phys. 2016;43:4915-4927.

45. Spindeldreier CK, Schrenk O, Bakenecker A, Kawrakow I, Burigo L, Karger CP, et al. Radiation dosimetry in magnetic fields with Farmer-type ionization chambers: determination of magnetic field correction factors for different magnetic field strengths and field orientations. Phys Med Biol. 2017;62:6708-6728.

46. Cusumano D, Placidi L, D’Agostino E, Boldrini L, Menna S, Valentini V, et al. Characterization of an inorganic scintillator for small-field dosimetry in MR-guided radiotherapy. J Appl Clin Med Phys. 2020;21:244-251.

47. Nelms BE, Chan MF, Jarry G, Lemire M, Lowden J, Hampton C, et al. Evaluating IMRT and VMAT dose accuracy: practical examples of failure to detect systematic errors when applying a commonly used metric and action levels. Med Phys. 2013;40:111722.

48. Sun B, Rangaraj D, Boddu S, Goddu M, Yang D, Palaniswaamy G, et al. Evaluation of the efficiency and effectiveness of independent dose calculation followed by machine log file analysis against conventional measurement based IMRT QA. J Appl Clin Med Phys. 2012;13:140-154.

49. Lamb J, Cao M, Kishan A, Agazaryan N, Thomas DH, Shaverdian N, et al. Online adaptive radiation therapy: implementation of a new process of care. Cureus. 2017;9:e1618.

50. Simon A, Nassef M, Rigaud B, Cazoulat G, Castelli J, Lafond C, et al. Roles of deformable image registration in adaptive RT: from contour propagation to dose monitoring. Annu Int Conf IEEE Eng Med Biol Soc. 2015;2015:5215-5218.

Fig. 1

Representative multi-leaf collimator (MLC) aperture shapes with the aperture area (AA), aperture irregularity (AI), aperture edge (AE), and beam-on time weighting factor (w) for each segment in the (A) breast IMRT and (B) abdomen SABR cases. In these sample apertures, the abdomen SABR plan showed the 190.4% higher beam area metric, and the 50.7% and 59.7% lower beam irregularity and beam edge metrics, respectively. IMRT, intensity-modulated radiation therapy; SABR, stereotactic ablative body radiotherapy.

Fig. 2

Scatter plots between the gamma passing rates (GPRs) with the 1 mm/2% criterion and various plan complexity metrics showing statistical significances: (A) modulation complexity score (MCS), (B) plan-averaged area metric (PA), (C) plan-averaged edge metric (PE), (D) average areas among all segments (AA/Seg), (E) total beam-on time (TBT), (F) total treatment time divided by daily dose (Time/DD), (G) proportion of the area less than 10 cm² among all segments (%SA/Seg<10), and (H) proportion of the segment with beam-on time less than 10 seconds among total number of segment (%Time/Seg<10).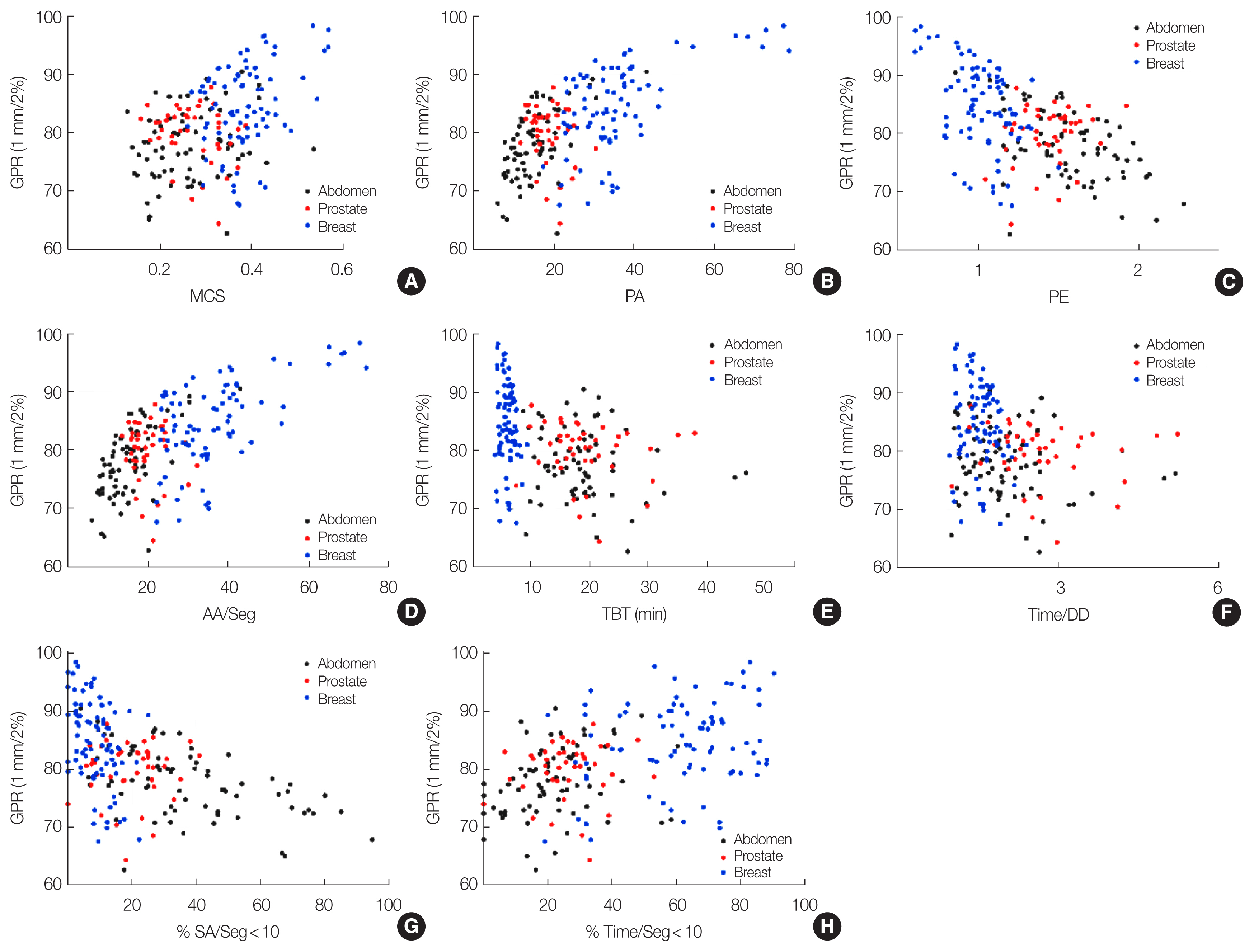

Table 1

Definition of the Plan Complexity Metrics

	Segment phase	Field phase	Plan phase	Study
MCS	LSVsegment=〈∑n=1N-1(posmax-\|posn-posn+1\|)(N-1)×posmax〉left×〈∑n=1N-1(posmax-\|posn-posn+1\|)(N-1)×posmax〉rightAAVsegment=∑a=1A〈posa〉left bank-〈posa〉right bank∑a=1A〈max(posa)〉left bank-〈max(posa)〉right bank∈field	MCSfield=∑i=1IAAVsegment,i×LSVsegment,i×Timesegment,iTimefield	MCS=∑j=1JMCSfield,j×Timefield,jTimetotal	McNiven et al. [4]
PA	AAsegment=T·∑a=1A〈posa〉left bank-〈posa〉right bank	BAfield=∑i=1IAAsegment,i·Timesegment,iTimefield	PA=∑j=1JBAfield,j·Timefield,jTimetotal	Du et al. [15]
PI	AIsegment=APsegment24π·AAsegment	BIfield=∑i=1IAAsegment,i·Timesegment,iTimefield	PI=∑j=1JBIfield,j·Timefield,jTimetotal	Du et al. [15]
PE	AEsegment=APsegmentAAsegment	BEfield=∑i=1IAEsegment,i·Timesegment,iTimefield	PE=∑j=1JBEfield,j·Timefield,jTimetotal	Younge et al. [36]
PM	N/A	BMfield=1-∑i=1IAAsegment,i·Timesegment,iU(AAsegment,i)·Timefield	PM=∑j=1JBMfield,j·Timefield,jTimetotal	Du et al. [15]

MCS, modulation complexity score; pos, leaf position; LSV, leaf sequence variability; AAV, aperture area variability; PA, plan-averaged area metric; T, width of the leaf (1.05 cm fixed); AA, aperture area metric; BA, beam area metric; AP, aperture perimeter of the MLC openings; AI, aperture irregularity metric; BI, beam irregularity metric; PI, plan-averaged irregularity metric; AE, aperture edge metric; BE, beam edge metric; PE, plan-averaged edge metric; BM, beam modulation metric; U(AA_segment,i), union area of all apertures in each field; PM, plan-averaged modulation metric.

Table 2

Average Plan Complexity Metrics according to the Treatment Sites, and their Statistical Significances across Groups

	Abdomen (n=71)	Prostate (n=41)	Breast (n=82)	p-value
	Abdomen (n=71)	Prostate (n=41)	Breast (n=82)	Breast vs. SABR	Abdomen vs. Prostate
MCS	0.26±0.08	0.27±0.06	0.39±0.07	<0.001	0.576
PA (cm²)	15.00±6.36	18.78±3.99	35.68±12.54	<0.001	0.000
PI	2.16±0.27	2.37±0.23	2.02±0.29	<0.001	0.000
PE	1.57±0.29	1.44±0.18	1.03±0.18	<0.001	0.004
PM	0.48±0.10	0.53±0.09	0.41±0.10	<0.001	0.008
#Seg	47.79±25.80	61.34±25.04	38.55±13.51	<0.001	0.008
AA/Seg	15.37±6.27	19.89±4.26	35.64±12.05	<0.001	0.000
TBT (min)	18.78±6.89	19.33±6.62	5.91±1.14	<0.001	0.722
Time/DD (min/Gy)	2.07±0.82	2.67±0.91	1.53±0.30	<0.001	0.000
%SA/Seg<2.5	2.74±3.40	1.71±2.05	0.53±1.19	<0.001	0.048
%SA/Seg<5.0	9.79±9.01	5.14±3.96	1.62±2.16	<0.001	0.000
%SA/Seg<7.5	19.48±14.87	9.84±5.83	4.37±3.89	<0.001	0.000
%SA/Seg<10.0	37.09±21.81	19.65±9.56	8.94±5.57	<0.001	0.000
%Time/Seg<3	2.47±3.64	3.42±2.53	11.33±6.38	<0.001	0.106
%Time/Seg<5	7.39±6.63	9.37±4.63	26.42±11.37	<0.001	0.066
%Time/Seg<10	21.74±13.31	26.10±10.58	61.03±18.03	<0.001	0.075

Values are presented as mean±standard deviation.

SABR, stereotactic ablative body radiotherapy; MCS, modulation complexity score; PA, plan-averaged area metric; PI, plan-averaged irregularity metric; PE, plan-averaged edge metric; PM, plan-averaged modulation metric; #Seg, total number of segment; AA/Seg, average areas among all segments; TBT, total beam-on time; Time/DD, total treatment time divided by daily dose; %SA/Seg<A, proportion of the area less than A cm² among all segments; %Time/Seg<T, proportion of the segment with beam-on time less than T seconds among total number of segment.

Table 3

Pearson Correlation Coefficients between GPRs with a 1 mm/2% Criterion and Plan Complexity Metrics

	Pearson correlation coefficient	p-value
MCS	0.416	<0.001
PA	0.627	<0.001
PI	−0.007	0.927
PE	−0.541	<0.001
PM	−0.084	0.242
#Seg	−0.035	0.624
AA/Seg	0.635	<0.001
TBT (min)	−0.397	<0.001
Time/DD (min/Gy)	−0.261	<0.001
%SA/Seg<2.5	−0.360	<0.001
%SA/Seg<5.0	−0.463	<0.001
%SA/Seg<7.5	−0.501	<0.001
%SA/Seg<10.0	−0.515	<0.001
%Time/Seg<3	0.442	<0.001
%Time/Seg<5	0.460	<0.001
%Time/Seg<10	0.470	<0.001

GPR, gamma passing rate; MCS, modulation complexity score; PA, plan-averaged area metric; PI, plan-averaged irregularity metric; PE, plan-averaged edge metric; PM, plan-averaged modulation metric; #Seg, total number of segment; AA/Seg, average areas among all segments; TBT, total beam-on time; Time/DD, total treatment time divided by daily dose; %SA/Seg<A, proportion of the area less than A cm² among all segments; %Time/Seg<T, proportion of the segment with beam-on time less than T seconds among total number of segment.